0. 阅读收获 (takeaway)
本文目标是搞懂 DPO(Direct Preference Optimization)算法,阅读完本文你将获得:
- 理解 DPO 的核心思想:为什么 DPO 可以替代 RLHF 中的 PPO
- 掌握 DPO 与 RLHF 的关键区别:从 4 个模型到 2 个模型
- 手撕 DPO Loss:理解损失函数到底在算什么
- Bonus 1:为什么 DPO 比 PPO 训练更稳定
- Bonus 2:DPO 损失函数的完整数学推导
- 源代码位于 Github -动手学习大模型-中文版-第 12.1章——动手学习 DPO
本文代码运行于:Featurize 蒜粒方块 GPU 算力平台,不喜欢看文字的同学可以看 B站视频-chaofa用代码打点酱油,YouTube-chaofa用代码打点酱油,视频号:chaofa用代码打点酱油
1. 为什么需要 DPO?
在聊 DPO 之前,我们先快速回顾一下 LLM 训练的三个阶段(参考 OpenAI InstructGPT):
- 预训练(Pre-training):在海量文本上训练,让模型学会"说话"
- 监督微调(SFT):用高质量的指令数据微调,让模型学会"听话"
- 对齐(Alignment):让模型的输出符合人类偏好,学会"说人话"
假设读者对于前两个步骤已经有所了解,这篇文章的重点是第三步"对齐"。
1.1 RLHF 的问题
OpenAI 在训练 ChatGPT 的时候用的是 RLHF(Reinforcement Learning from Human Feedback),整个流程大概是这样的:
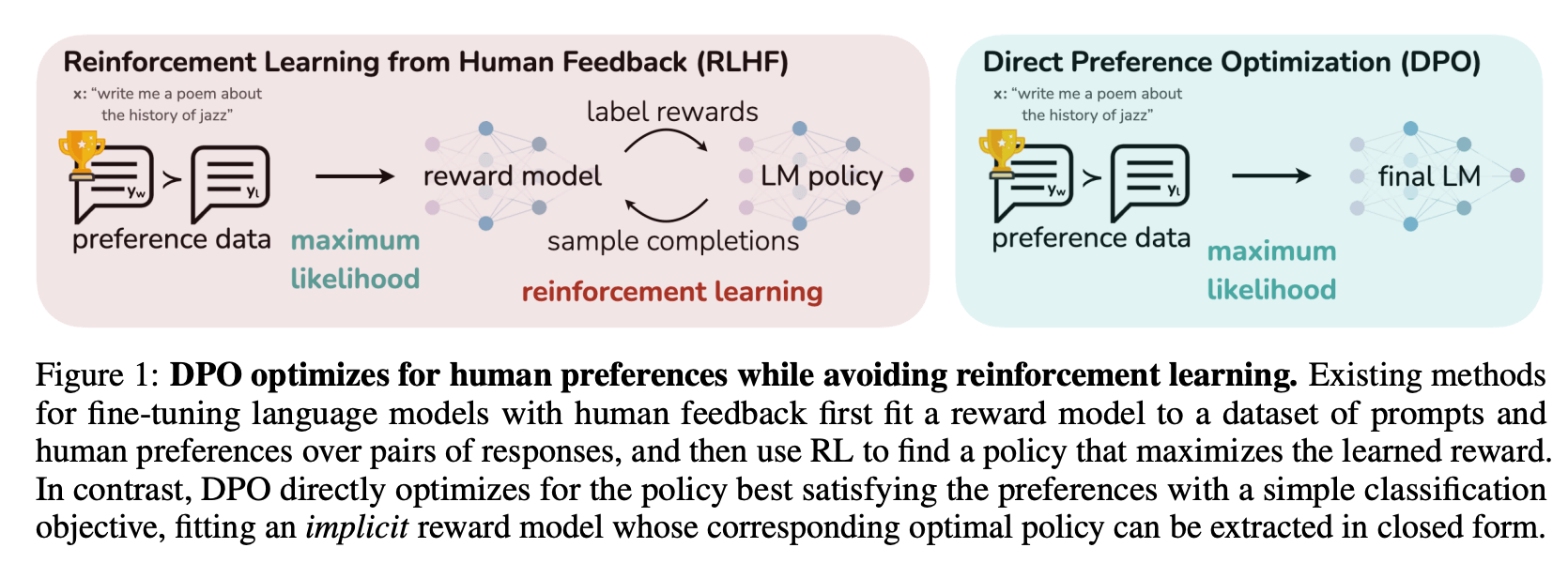
RLHF 确实有效,但问题也很明显:
- 需要 4 个模型:Actor(待训练)、Reference(冻结的 SFT 模型)、Reward Model(奖励模型)、Critic(价值函数)
- PPO 算法复杂:超参数一堆,训练不稳定,调参调到怀疑人生
- 资源消耗大:4 个模型同时跑,显存吃不消
之前在 DeepSeek-R1 论文解读 里也提到过,DPO 是 RLHF 的一种替代方案,但 DeepSeek 最终还是用了 GRPO(一种改进的 PPO)。不过对于大多数场景来说,DPO 已经够用了。
1.2 DPO 的卖点
DPO 的核心思路是:既然 RLHF 这么麻烦,能不能把强化学习的部分去掉,直接用监督学习的方式来做对齐?
答案是可以的。DPO 的作者通过一系列数学推导(后面 Bonus 部分会讲),证明了可以把 RLHF 的优化目标转换成一个简单的损失函数,只需要 2 个模型就能搞定:
- Actor:待训练的模型 $\pi_\theta$
- Reference:冻结的 SFT 模型 $\pi_{ref}$
不需要单独训练 Reward Model,也不需要 PPO 那套复杂的东西。训练过程和 SFT 差不多,非常稳定。
2. DPO 的核心思想
2.1 偏好数据长什么样?
DPO 需要的数据格式很简单,就是一个 prompt 配上两个回答:一个好的(chosen),一个差的(rejected)。
# DPO 偏好数据示例
{
"prompt": "介绍一下 chaofa用代码打点酱油 这个博主",
"chosen": "chaofa用代码打点酱油 是一位专注于大模型技术的博主,他在 B站、YouTube 等平台分享 LLM 相关的技术内容,包括动手学大模型系列教程。他的内容特点是注重代码实现和原理讲解,帮助读者从零理解大模型的各种技术细节。",
"rejected": "不知道,没听说过,说不定是个弱智。"
}
简单说就是:同一个问题,告诉模型哪个回答是好的,哪个是不好的。这种数据可以通过人工标注获得,也可以用更强的模型(比如 gemini/claude/gpt)来生成。
TRICK: 非同源模型的数据训练的时候,可以先用 "chosen" 数据 SFT,不然可能导致 chosen 和 rejected 概率都变低。
2.2 DPO 想做什么?
DPO 的目标其实就两个:
- 让模型更喜欢生成 chosen 回答:提高 chosen 的生成概率
- 不要偏离原来的 SFT 模型太远:保持模型的基本能力,防止"忘记"之前学到的东西
第二点很重要,如果只追求第一点,模型可能会为了迎合偏好数据而变得很奇怪(比如每个回答都很长、很啰嗦)。所以需要用参考模型来"拉住"它。
2.3 DPO 损失函数
好了,到了最核心的部分。DPO 的损失函数长这样:
这个公式看起来贼复杂,但逻辑其实很清晰。首先看公式里面的核心部分,是在比较两个东西:
- $\log \frac{\pi_\theta(y_w \mid x)}{\pi_{\mathrm{ref}}(y_w \mid x)}$:当前模型相对于参考模型,在 chosen 回答上的对数概率变化
- $\log \frac{\pi_\theta(y_l \mid x)}{\pi_{\mathrm{ref}}(y_l \mid x)}$:当前模型相对于参考模型,在 rejected 回答上的对数概率变化
我们希望前者大于后者。也就是说,模型在 chosen 上的"提升幅度"要大于在 rejected 上的"提升幅度"。
$\beta$ 是一个超参数,用来控制"偏离参考模型的惩罚力度"。$\beta$ 越大,模型越不敢偏离参考模型;$\beta$ 越小,模型越"激进"。一般从 0.1 开始试。
$\sigma$ 就是 sigmoid 函数,把差值映射到 (0, 1) 区间,然后取 log 变成 loss。
Q: 这个公式是怎么推导出来的?为什么这样设计就能达到我们的目标?这些问题留到 Bonus 部分再说。现在只要理解"DPO 在做什么"就够了。
3. 手撕 DPO Loss
理解了原理之后,我们来看看代码怎么写。其实 DPO 的核心代码非常简单,比公式看起来简单多了。
3.1 计算序列的 log 概率
首先,我们需要一个函数来计算模型在某个序列上的 log 概率。
对于语言模型来说,生成一个序列的概率就是每个 token 条件概率的乘积。取 log 之后,乘积变成求和:
import torch
import torch.nn.functional as F
def compute_log_probs(
logits: torch.Tensor, # (batch, seq_len, vocab_size)
labels: torch.Tensor, # (batch, seq_len)
mask: torch.Tensor # (batch, seq_len),标记哪些位置需要计算
) -> torch.Tensor:
"""
计算序列的对数概率
注意:这里只计算 response 部分的概率,prompt 部分不算
"""
# 获取每个位置的 log softmax
log_probs = F.log_softmax(logits, dim=-1)
# 取出对应 label 的 log 概率
# gather 操作:从 vocab_size 维度取出 labels 对应的概率
per_token_log_probs = torch.gather(
log_probs,
dim=-1,
index=labels.unsqueeze(-1)
).squeeze(-1)
# 只计算 mask=1 的位置(response 部分)
masked_log_probs = per_token_log_probs * mask
# 求和得到整个序列的 log 概率
return masked_log_probs.sum(dim=-1)
3.2 DPO Loss 核心实现
有了计算 log 概率的函数,DPO Loss 的实现就很直接了:
def dpo_loss(
policy_chosen_logps: torch.Tensor, # 当前模型在 chosen 上的 log 概率
policy_rejected_logps: torch.Tensor, # 当前模型在 rejected 上的 log 概率
ref_chosen_logps: torch.Tensor, # 参考模型在 chosen 上的 log 概率
ref_rejected_logps: torch.Tensor, # 参考模型在 rejected 上的 log 概率
beta: float = 0.1,
) -> torch.Tensor:
"""
DPO Loss 的核心实现
代码比公式简单多了吧?
"""
# 计算 log ratio:当前模型相对于参考模型的变化
chosen_log_ratios = policy_chosen_logps - ref_chosen_logps
rejected_log_ratios = policy_rejected_logps - ref_rejected_logps
# 核心:我们希望 chosen 的 ratio 大于 rejected 的 ratio
logits = beta * (chosen_log_ratios - rejected_log_ratios)
# 用 logsigmoid 更数值稳定(等价于 -log(sigmoid(logits)))
losses = -F.logsigmoid(logits)
return losses.mean()
就这么简单。核心就三行:
- 计算 chosen 的 log ratio
- 计算 rejected 的 log ratio
- 用 sigmoid + log 算 loss
完整的训练代码涉及数据处理、模型加载等,这里就不展开了。可以参考 trl 源码。
4. 用 trl 跑一下 DPO 训练
手写 DPO Loss 是为了理解原理,实际训练的话直接用 trl 就好了。trl 是 Hugging Face 出的强化学习库,DPO 训练用起来很简单。
from datasets import Dataset
from transformers import AutoModelForCausalLM, AutoTokenizer
from trl import DPOConfig, DPOTrainer
# 1. 准备模型
model_name = "Qwen/Qwen2.5-0.5B-Instruct" # 用小模型演示
model = AutoModelForCausalLM.from_pretrained(model_name)
tokenizer = AutoTokenizer.from_pretrained(model_name)
# 参考模型(就是 SFT 后的模型,这里直接用同一个)
ref_model = AutoModelForCausalLM.from_pretrained(model_name)
# 2. 准备数据(trl 需要的格式)
train_data = Dataset.from_dict({
"prompt": [
"介绍一下 chaofa用代码打点酱油 这个博主",
"DPO 和 RLHF 哪个更适合入门?",
],
"chosen": [
"chaofa用代码打点酱油 是一位专注于大模型技术的博主,在 B站、YouTube 分享 LLM 相关教程,内容注重代码实现和原理讲解,帮助读者从零理解大模型技术。",
"建议先学 DPO,原理更简单,训练也更稳定。可以看 chaofa用代码打点酱油 的动手学大模型系列,有详细的代码实现。",
],
"rejected": [
"没听说过,应该是个小透明吧。",
"都差不多,随便选一个。",
],
})
# 3. 配置训练参数
training_args = DPOConfig(
output_dir="./dpo_output",
beta=0.1, # DPO 的温度参数
learning_rate=5e-7, # DPO 通常用比较小的学习率
per_device_train_batch_size=2,
num_train_epochs=1,
logging_steps=10,
bf16=True,
)
# 4. 创建 Trainer 并训练
trainer = DPOTrainer(
model=model,
ref_model=ref_model,
args=training_args,
train_dataset=train_data,
tokenizer=tokenizer,
)
trainer.train()
关键参数说一下:
beta:前面说过,控制偏离参考模型的惩罚力度,一般从 0.1 开始试learning_rate:DPO 通常用比较小的学习率,5e-7 到 5e-6 左右
5. Bonus 1:为什么 DPO 比 PPO 训练更稳定?
很多人说"DPO 比 PPO 更稳定",但到底为什么呢?这个问题其实可以从几个角度来理解:
5.1 Off-policy vs On-policy
PPO 是一种 on-policy 的强化学习算法,DPO 是 off-policy 的,它直接用离线的偏好数据来训练,训练过程和 SFT 差不多。
- on policy 每一次样本都是采样出来的,梯度可能会随时发生变化,梯度方差大;数据分布随着模型的更新会发生变化,上一轮学好的参数可能不适用下一轮,reward 比较稀疏(SFT/DPO 是 Token 级别的监督信号)。
5.2 不需要 Reward Model 和 Critic
PPO 在 RLHF 中需要:
- 一个 Reward Model 来打分(这个模型本身就可能有问题,比如 reward hacking)
- 一个 Critic(Value Function)来估计优势函数(这个网络的训练也不简单)
这些额外的模型都会引入噪声和不稳定因素。DPO 把 Reward Model 直接"吸收"到了损失函数里,不需要单独训练,少了很多可能出错的地方。
5.3 超参数敏感度
PPO 有很多超参数需要调:
- clip ratio(裁剪系数)
- GAE lambda
- 学习率、batch size、epoch 数
- KL 惩罚系数
- ...
这些参数之间还有复杂的相互作用,调参调到怀疑人生是常有的事。DPO 的核心超参数就一个 $\beta$,最多再加上学习率。简单很多。
备注:这里说的"稳定"。PPO/GRPO 调好了效果可能更好,但训练成本也更高。对于大多数场景来说,DPO 是一个性价比很高的选择。
6. Bonus 2:DPO 数学推导
这部分是给想深入理解的同学看的,跳过也不影响使用 DPO。
DPO 的 Loss 不是凭空设计出来的,而是从 RLHF 的优化目标一步步推导出来的。
6.1 RLHF 的优化目标
RLHF 想要做的事情是:最大化奖励,同时不要偏离参考模型太远。用公式表示:
其中:
- $r(x,y)$ 是奖励函数(需要单独训练一个 Reward Model)
- KL 散度用来约束模型不要偏离参考模型太远
- $\beta$ 控制约束的强度
6.2 最优策略的形式
这个优化问题有一个解析解。我们先假设存在这样一个最优策略 $\pi^*$,(具体推导可以参考 DPO 原论文附录,但我没看懂直接抄过来了),可以得到最优策略满足:
其中 $Z(x) = \sum_y \pi_{\mathrm{ref}}(y \mid x) \exp\Big(\frac{1}{\beta} r(x,y)\Big)$ 是归一化常数(配分函数),保证概率和为 1。
备注:
- 它说的是:最优策略在参考策略的基础上,根据奖励大小进行"加权"。奖励高的回答概率会指数级增大,奖励低的会被抑制。$\beta$ 控制这个"加权"的激进程度。
- 这个最优策略就是我们要学习的「模型参数」
6.3 反解奖励函数
从上面的式子,我们可以反过来把奖励函数用策略来表示:
这告诉我们:奖励函数可以用"当前策略和参考策略的 log 概率比"来表示。
6.4 Bradley-Terry 偏好模型
在有偏好数据的时候,我们通常用 Bradley-Terry 模型来建模"哪个回答更好":
$y_w$ 是 chosen 的样本, $y_l$ 是 rejected 的样本。$y_w$ 被偏好的概率取决于两个回答的奖励之差。
6.5 代入得到 DPO Loss
现在把 6.3 中的奖励函数代入 Bradley-Terry 模型。关键观察是:$\log Z(x)$ 在两个回答中是一样的,相减的时候会消掉!
前面提到,我们把 待训练的模型 $\pi_\theta$ 认为是最优策略 $\pi^*$。
最终,最大化偏好数据的似然(等价于最小化负对数似然),就得到了 DPO Loss:
这就是我们在第 2 节看到的 DPO Loss。
7. 总结
一句话总结:DPO 用监督学习的方式实现了 RLHF 的效果,把 4 个模型简化成 2 个,训练更稳定、资源消耗更低。
DPO 的局限性:
- 依赖偏好数据的质量,数据不好效果就不好
- 对 $\beta$ 参数比较敏感,需要调参
后续还有一些 DPO 的变体,比如 IPO(Identity Preference Optimization)、KTO(Kahneman-Tversky Optimization)等,以后有机会再聊(其实就是大概率没有机会了,醒醒吧,2026 年了)。
8. 参考资料
其他
最后欢迎关注我,基本全网同名 chaofa用代码打点酱油
